Part 1 Payout Planning for Variable Markets
- Cam Anderson

- Oct 31, 2022
- 6 min read
Updated: Dec 11, 2022
At the root of all the articles in this blog is the desire to make growing, repeating payouts that benefit society, so it is worth diving much deeper into the details of the process of making payouts.
Payouts must vary with unpredictable investment results yet support donor intentions. This article is part one of a two-part article to illustrate how to accommodate a range of donor objectives and payout amounts that robustly withstands the wildest 25-year market gyrations. Next month, the second article will present how best to calculate the payout amounts and the donor planning implications.
Growth rate update
I begin with an update on the expected growth of investments. Last month’s article about ‘Estimating future growth rates' uses 102 data intervals representing 25-year growth results based on the Dow Jones index. The Median Net Compound Annual Growth Rate (CAGR) from those results was 4.729%, net of costs, tax and inflation.
Since then, I have reconsidered how best to reflect inflation. I redid my calculations to include actual CPI inflation year by year with the Dow Jones growth in each 25-year calculation because inflation and market performance influence each other. The new Median Net CAGR increases to 5.27% from 4.729%. This difference may seem small, but over time has a significant influence on the average expected results.
Recall that in determining the growth rates last month, we recommended using a 25-year cycle period that coincides with significant anniversaries we traditionally celebrate. Also, 25 years represents the approximate distance between generations. A typical cycle starts with an investment of seed funds for 25 years until the anniversary date, when the actual CAGR% is measured. Using the CAGR%, we determine the appropriate payout to charity for the growth that occurred. The fund balance after the payout is the revised ‘seed fund’ that is reinvested for a new 25-year cycle.
At a 5.27% growth rate, investments increase to more than triple the invested money in 25 years. Such average results reflect the likely outcome over many instances but do little to describe how payouts should be structured in the shorter term of, say, the first ten or more 25-year periods.
Market variability
The reality is that markets are unpredictable, and individual period results can vary wildly. Updating last month’s blog, our expected 25 Year Net CAGR, after including inflation and deducting 1.9% in costs (for investment management, administration, and taxes on investment income), varies over the 102-year study from 0.4% to 9.85%. In other words, for any given 25-year period, the results could vary from practically no net return to a great return.
Given this wide range of growth results, donors and future generations need to know the optimal portion at each anniversary to payout as the gift to charity, with the remainder reinvested.
What results are expected?
A convenient way to simplify the situation is to group the growth variation generated results by multiples of the invested funds. As seed funds grow over each 25-year cycle, the eventual real dollar size can exceed as much as ten times the cycle’s seed funds.
Step one to create such groupings is to compute the average growth rates required to generate an exact whole number multiple over 25 years, which are:
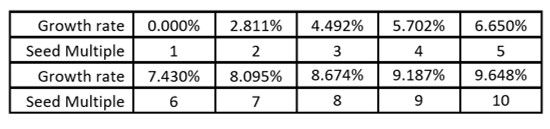
Next, we organize the actual 102 instances of 25-year CAGR growth rates into groups of seed fund multiples:
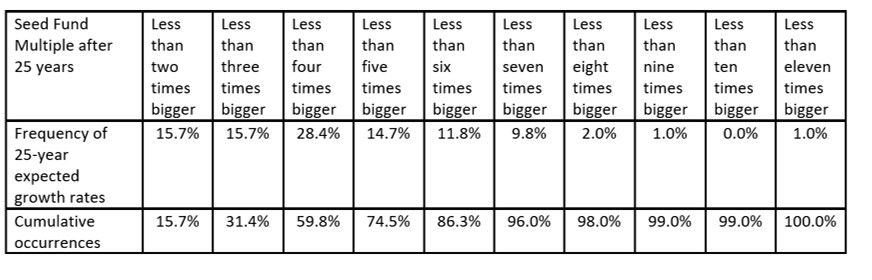
To explain the second table above, looking at the leftmost result, 15.7% of the 102 instances of future real-dollar-after-costs results will be less than two times the seed money invested at the start of the 25-year period. 15.7% of the measured CAGR growth rates are less than 2.811% (as shown in the first table). The yield for 15.7% of 25-year periods will be less than two times the seed money.
Similarly, 28.4% of 25-year results, as shown in the third column, will be above three times the multiplier growth rate of 4.492% but less than the growth rate of 5.702% to be a four times multiplier. Cumulatively 59.8% of individual random CAGR 25-year results will be less than the four times multiplier.
The good news is that 68.6% (100% less 31.4%) of the 25-year results will exceed the three-time multiplier, sometimes by quite a bit, suggesting that results could be impressive over the long term.
How much should payouts be?
Payouts at each anniversary interval depend on the specific investment period results achieved but are primarily driven by the donor’s gift objective. I propose three donor gift objectives as follows:
Maximum Gift (No Growth): If a donor has the financial power to start giving away a considerable sum immediately, the goal is to give that large sum repeatedly every 25 years. No growth in the size of the repeating donations is sought. The gift given can be up to, but must never reduce, the seed fund’s original real dollar value at each payout point. Market averages will result in a constant gift in absolute dollars, but averages are over many periods, not single cycles.
When donors want to specify a maximum repeating gift, they target the 25-year invested seed fund, not the gift. This donor-set target is not based on the gift amount, even though the “plan” is to have a constant amount repeatedly given because individual market 25-year cycles determine the gift size for that cycle. The Maximum Gift in any 25-year period would vary from zero to nine times the seed reinvested funds due to fluctuations in market performance, whereas the seed fund amount is constant.
Reaching a Maximum Gift payout must be the eventual steady state for all donor programs. Most donors will start with less than desired maximum average payout money. Instead, these donors set a Maximum Gift Seed Fund target that balances the trade-off between the size of a repeating gift and the time needed to achieve it.
Minimum Gift (Fastest Growth): Most donors less financially endowed will want Maximum Gift seed funds to be many multiples more than the Original seed fund size they first contributed. For example, a donor could specify amplifying their original gift by a factor of 1,000 (likely taking seven or more 25-year cycles) before converting to a Maximum Gift program.
By setting the payout level equal to the Original seed donation for all Minimum Gift cycles, with the balance reinvested, the funds compound rapidly every 25 years. After several cycles, the seed fund will eventually reach an amount to switch the payout program to the donor-defined Maximum Gift level.
Donors should specify the size of the Maximum Gift seed funds they desire at the plan inception so future generations have guidance for switching from Minimum Gift to Maximum Gift.
To ensure the continuity of the program, I would also suggest an absolute peak seed fund per donor to be $500 Million. At this level, the individual’s influence over others is not undue compared to someone who might pick a number in the hundreds of billions or trillions as an end target. Such huge numbers would take a long time to achieve and be much riskier to potential fraud and political interference.
Theoretically, the minimum gift at each 25th anniversary could be zero, allowing the maximum re-investment and maximum fastest growth. Donors could adopt that approach, but I suggest giving some funds every 25 years so a gift becomes expected and looked forward to by each subsequent generation. As discussed in an earlier article, this public visibility and support is crucial to minimizing fraud and theft issues.
Medium Gift (Slower Growth) is the in-between approach, neither Maximum Gift nor Minimum Gift. This slower growth path is ideal if the donor wants to give more sooner before achieving the Maximum Gift level.
In this case, one possibility is that half the 25-year increase be given out as a payout and half reinvested. Such an even balance between the needs of the present and future displays a certain intergenerational fairness. The Medium Gift payout gives more sooner than the Minimum Gift stage but reaching the Maximum Gift stage takes twice the time. Other Medium Gift possibilities could reduce or increase the portion paid out between the Minimum and Maximum levels.
The table below summarizes the recommended gifts per payout, given the growth multiple experienced during any particular 25-year period.
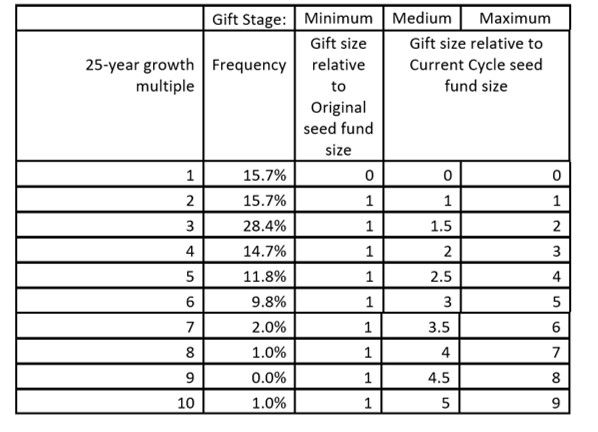
As nearly zero growth happens in 15.7% of 25-year intervals, zero payouts, in that case, are recommended regardless of the growth stage. This zero result is expected and typical for a long-run program which also gives four or more invested fund multiples more than 25% of the time but still, this will be disappointing when it happens.
One possibility to reduce the number of zero payout cycles could be adding groupings other than whole number multiples. For example, in the 15.7% less than two multiples group, a 50% seed fund payout is possible for 4.9% of cycles, and a 25% payout for 6.9%, reducing the zero payouts to only 3.9% [i] of the total cycles.
Another consolation is that based on historical data of 23 instances, only 2 cases had a subsequent 25-year zero payout. The rest, on average, had a four times gift multiplier in the following 25-year period.
In Summary
While the length of the payout period cycle and portions given and reinvested are infinitely variable, the fundamental principle is that the actual value of the seed fund must not be reduced. Only by protecting the seed fund value does the program eventually pay off.
Donor payout plans that follow the above recommendations within the related gift stage and growth multiple will create generous payouts and yet meet donor objectives for whatever variable markets may follow.
Next month I continue this payout plan discussion by addressing the following:
1. How would these payouts be calculated in the future?
2. Under these scenarios, what are the likely real-dollar gift results?
3. How might donors best specify their plan?
Your comments and ideas are most welcome at Cam@FutureLegacies.ca. Thanks for reading!
[i] Calculated by 15.7% minus 4.9% minus 6.9%





Comments