The magic of compound growth
- Cam Anderson

- Apr 23, 2020
- 8 min read
Updated: Nov 10, 2020
How is a large amount of money raised to help society. The secret lies in the complex term "compound growth".
The magical powers of compounding
Compound growth is a difficult concept. It is the power behind raising money, building a movement, greening the planet, and even spreading a virus, yet we struggle to understand this. We humans project well linearly but find it nearly impossible to anticipate or forecast exponentially. Not because we are incapable, but it is not easy to estimate.
As an example, if we drive at 60 km per hour, we can easily extrapolate to say in one hour we will have traveled 60 kilometers. After two hours we will cover 120 kilometers.
But if we are accelerating, we are speeding up. If our car starts at 60 km per hour and accelerates one kilometer per hour every minute, we will be at 120 km per hour at the end of the hour. How far we traveled is a function of the average speed of the journey. Still, this example is a linear projection of 90 km average speed and thus covering 90 km over one hour.
Now say the rate of the car's acceleration is accelerating too. Imagine the car's acceleration is increasing by one kilometer per hour per minute. That car would be going 61 kmh the first minute, 63 kmh the second, 66 kmh the third, and so on. Try to guess the final speed of the car after one hour, or the distance covered in this scenario. We can solve this, but not usually in our heads. The final speed after one hour? 31 km per minute, or 1,890 kmh. Total distance covered? 675 km in one hour.
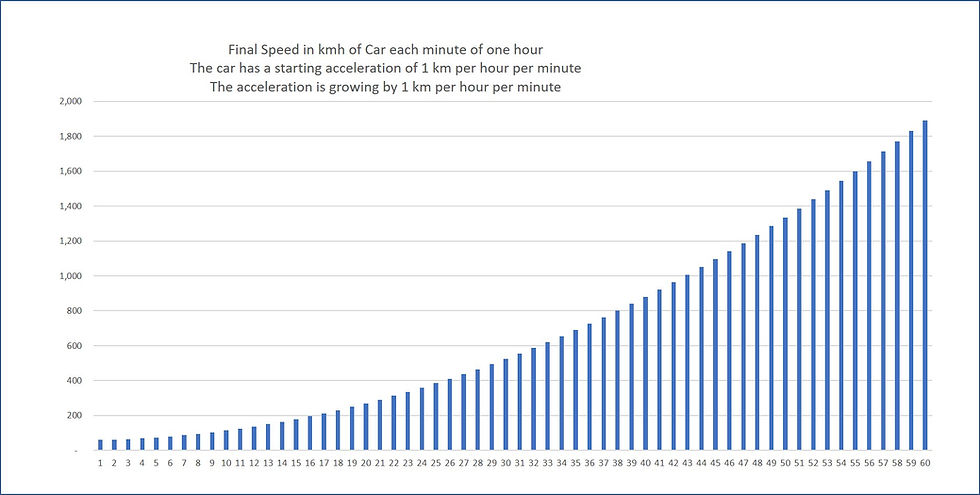
What is interesting is our early impression of the car's speed. In the first 10 minutes, the vehicle reaches 100 kmh or an increase of only 41 kmh. In the last 10 minutes of the hour, the car increases speed by a whopping 555 kmh. Speed increases by orders of magnitude the later that we measure. Simply projecting in a linear fashion does not work here. Consequently we are liable to underestimate the final result.
The danger in minimizing impact:
Planning pandemic response levels from early COVID-19 case counts is very misleading. In unrestricted spread mode, the virus has shown it can double the number of cases every 3 days. Starting with one case, it takes three weeks to reach one hundred instances. At this rate of growth, about every 10.5 days the number of cases grows by a factor of 10. After 60 days, the number of cases reaches a million, 70 days 10 million, 80 days 100 million, 90 days 1 billion.
Isolation, social distancing, and contact tracing can dramatically slow the virus's spread. If we restrict growth in cases to doubling every ten days, after 62 days, the total cases are 100. That is 10,000 times smaller! And after 90 days? Just 900 cases.

So getting the virus accurate growth rate early on is critical, yet difficult due to lack of data. Many world leaders could not get behind the social and economic impacts of shutting down, especially when only a hundred cases appear after 21 days. The concerns to them must have seemed trivial, and so many leaders, unfortunately, chose bravado over math.
The speed of doubling is critical.
Which would you pick? Once my teacher asked which I would prefer, one penny doubling every day for a 30 day month, or $100,000. I naturally chose the $100,000. This choice is affected by the perception error we typically fall into. A large number relative to the initial sample (in this case, one penny) makes the obvious choice the more significant amount.
The actual result is staggering. After 30 days of doubling, the penny becomes $5,368,709.12.
The interesting thing about money doubling every day is that half the money grows in the account on the last day. In the previous 3 days or last 3 doublings, 87.5% of the money is added. In the last six days, 98%.
Here is a chart of the last ten days. Notice how small the 21st day's size is relative to the 30th day's size:
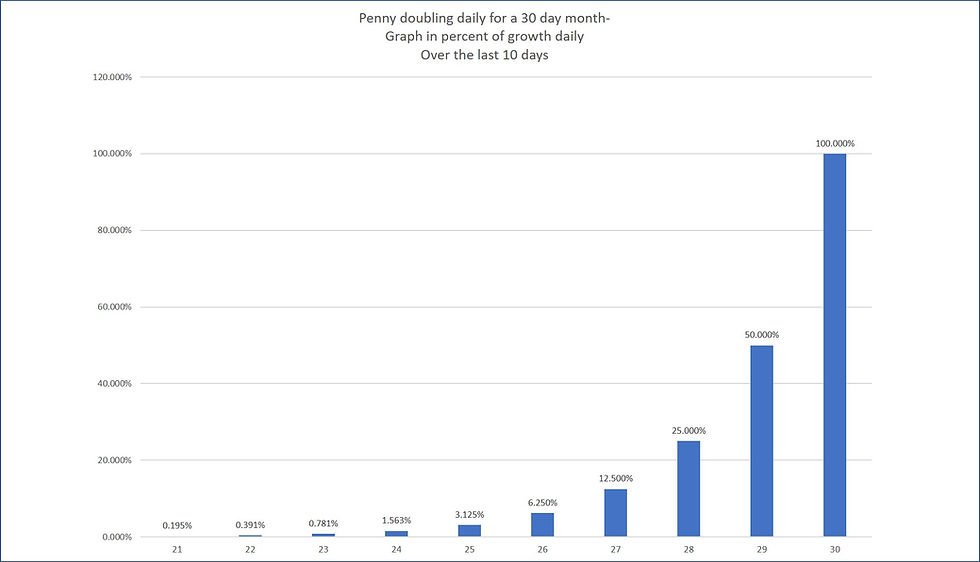
The lesson from the above chart is that once you get to 50% or 100%, you have magnitude and not before. The implication is that a large sum once reached can propel on and on, rather quickly.
Growing Seed Fund
I recommend Seed Funding Corporations in order to raise seed money for Charitable Foundations. These funds can happen only by using compound growth. And that same compound growth tool also applies to personal money growth.
Compound growth doubling in personal financial situations is frustratingly slow. Turning 100 dollars into 1,000,000 dollars takes way too long. It's an increase by several orders of magnitude. Ever wish you could just stare at a bank account and make it slide over only one little zero? I have.
To estimate how long a period is required for savings to double financial planners use the "Rule of 72". This rule states funds double when the rate of growth times the years of growth equals 72. So if you know the growth rate is 10 percent, then the number of years to double this growth is 72/10 or 7.2 years. Or conversely, if you know the funds doubled in 7.2 years, then the growth rate was 10 percent.
Bill Gates has a wealth exceeding $50 Billion. If he invests his funds at 10 percent, the $50 Billion becomes $100 Billion using the rule of 72, in just 7.2 years.
An extension on the rule of 72 is the "Rule of 230," whereby any number will grow by a factor of 10. So if you know the rate of growth is 10% per year, then the number of years required to add a zero is 230/10 = 23 years.
Now if Bill Gates does nothing but invest funds at 10 percent, the 50 Billion becomes 500 Billion in 23 years. That's the power of compounding when a sizable starting point energizes it.
The starting point is equally important as the growth rate. Doubling a penny is nothing compared to doubling one million, yet both take the same amount of time, and both result in a doubling from the starting point.
What if once we got to a certain size of fund, we let it double over and over. Each time it would double, we could assign half to a charity, and then let the funds double again. Since charities will always be with us, setting this up can act like money pump that pours in new money to charity with every doubling.
More on the concept of perpetual doubling below. But first let's discuss how much a charity can use each year of a large sum in a foundation.
Withdrawal rates
Financial planners agree that spending around 4% of a savings plan in retirement is a sustainable proposition. This same 4% annual spend can apply to charities spending money held in investments by charitable foundations. Here is why the 4% number makes sense:
The Standard and Poor's 500, or simply the S&P, is a stock market index that measures the stock performance of 500 large companies listed on stock exchanges in the United States. It is one of the most commonly followed equity indices, and many consider it to be one of the best representations of the U.S. stock market. The Annualized S&P 500 Return (Dividends Reinvested) is 9.955% since the index began in 1957.
If we assume our savings will achieve a 9% annual return over the long run, recognizing some years results are miserable, some are amazing and we pay approximately 1% to an investment advisor and 1% in annual taxes as the stocks are sold and reinvested, we have 7% net growth before inflation. With inflation running around 2% to 3%, this means our fund will grow at a net rate of 4% to 5% each year.
If we annually withdraw just 4%, the fund's original amount remains unreduced. And better still, it means using 4% as an annual spending budget is relatively a safe proposition.
What can we do with this?
Knowing that annually spending 4% is sustainable, we can work backward to estimate how much savings are needed.
Say a charity would like a foundation that provides $10 Million per year, sustainably. The $10 Million, in this case, is the annual spend, or 4% of the foundation's portfolio. Therefore the portfolio needs to be 25 times (100% / 4%) the annual spend, which in this case is $250 Million
Perpetual doubling.
Once we reach a significant fund size, the fund value has critical mass for what I call 'Perpetual Doubling,' meaning perpetually doubling 50% of the investment funding. After each doubling, half is reinvested to double again, and half is donated to a foundation. The foundation grows by these large increments with every doubling. The result is that 4% of the foundations' funds now also rises with every doubling.
Let's say Bill Gates fortune doubles in 14 years, adding $50 Billion in the process. If he wants to donate it all, he could choose to double the funds perpetually. So instead of giving all $50 billion to charity at first, he only provides half, $25 B, then the other half can continue to grow inside a Seed Corporation investment fund.
Immediately at 4%, the $25 B is sustainably funding $1 Billion annual spend. The additional $25 B investment fund grows, until after another 14 years, it reaches $50 Billion. Again $25 B is added to the charity, adding effectively another ongoing $1 B a year to the charity annual budget. In this way, the sustainable funding for the charity goes up sustainably by $1 B every 14 years.
One could argue that setting up perpetual doubling delays the cash flow to the charity that could have been set to and on-going 4% of the full $50 Billion, or $2 Billion annual perpetually. Yes this is true.
The Perpetual Doubling delay in value received by those in need today must be weighed against the ever expanding value to meet needs in future. In part the new donation today should be net new, and thus quite welcome today at any level. That half is set aside to ever expand capability to meet societal needs every 14 years, should be the a desirable outcome for both now and the near future.
Funding charitable foundations
Recall in our example above the charity wanted $10 Million per year, requiring a foundation fund of 25 times bigger, $250 Million.
If a donor gives a legacy at passing on of $2.5 Thousand, the goal would be to add five orders of magnitude, five zeros, to reach $250 Million. At 5% net growth after inflation, and using the rule of 230, the fund would add a zero every 46 years. Repeating this five times, once per zero, means the charitable foundation would need 230 years to grow $2.5 thousand to reach the target $250 Million.
The top 60 percent of the average Canadian household has a net worth exceeding $300 K, so $2.5 Thousand is less than 1 percent. We have 85 thousand Registered Canadian charities, all of which could be targets for such legacies. If 85 thousand such gifts are made and left for 250 years, the fund reaches a staggering value of $21 Trillion. We can expect to fund all 85,000 of these charities sustainably with $10 Million forever after. That is a total of $850 Billion a year, far higher than our current donations level of $10.6 B per year
The collective group reaches the target $10 B per year much sooner, about 100 years earlier. The supporting fund would need to reach $250 Billion. We, however, know we would like to see a higher level than just the $10 B per year. If, after the first 150 years, we wait for one more doubling of the supporting fund, the $250 B turns into $500 B. At 5 %, this would take 14 years to double. Setting aside then $250 B for more growth of the $500 B, allows perpetual doubling each subsequent period to add $10 B new funds to the charities. This provides a strong base that is ever-growing in support of Canadian Charities.
How might this target fund level be reached even sooner?
Let's think big. Set a target for $250 Billion then borrow $ 35 Billion. The interest cost is 4%. After paying interest, the $35 billion grows to $ 60 Billion in 20 years. Payback the loan and allow the remaining 25 Billion to grow at 5%. It would take 46 years more to reach $250 Million, and 14 years further to set up perpetual doubling. The total time required is 80 years.
As you can see, the more you begin with, the quicker the results.
Compound growth is our lever to solve many of the problems of the world
Photo by Micheile Henderson on Unsplash





Comments